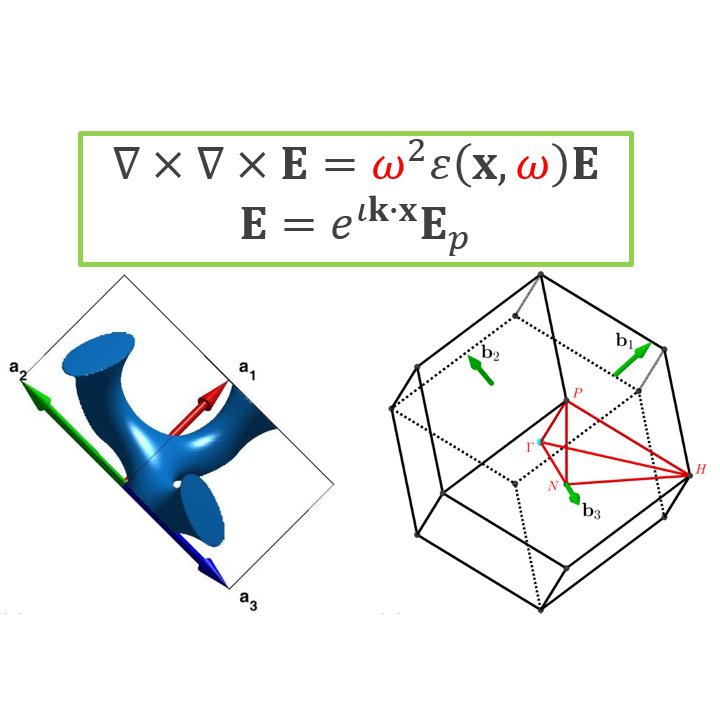
This work is devoted to the numerical computation of complex band structure 𝐤=𝐤(𝜔)∈ℂ^3 for positive frequency 𝜔 of 3D isotropic dispersive or non-dispersive photonic crystals from the perspective of gyroscopic quadratic eigenvalue problems (GQEPs). Our basic strategy is to fix two degrees of freedom in k and to view the remaining one as the eigenvalue of a quadratic operator pencil derived from Maxwell's equations. Then Yee's scheme is employed to discretize ∇×and 𝒌× operators in this quadratic operator pencil. Furthermore, we reformulate this QEP into an equivalent T-palindromic QEP (T-PQEP) for which we have established the structure-preserving algorithm, namely, the generalized T-skew-Hamiltonian implicit restarted Arnoldi algorithm (GTSHIRA).